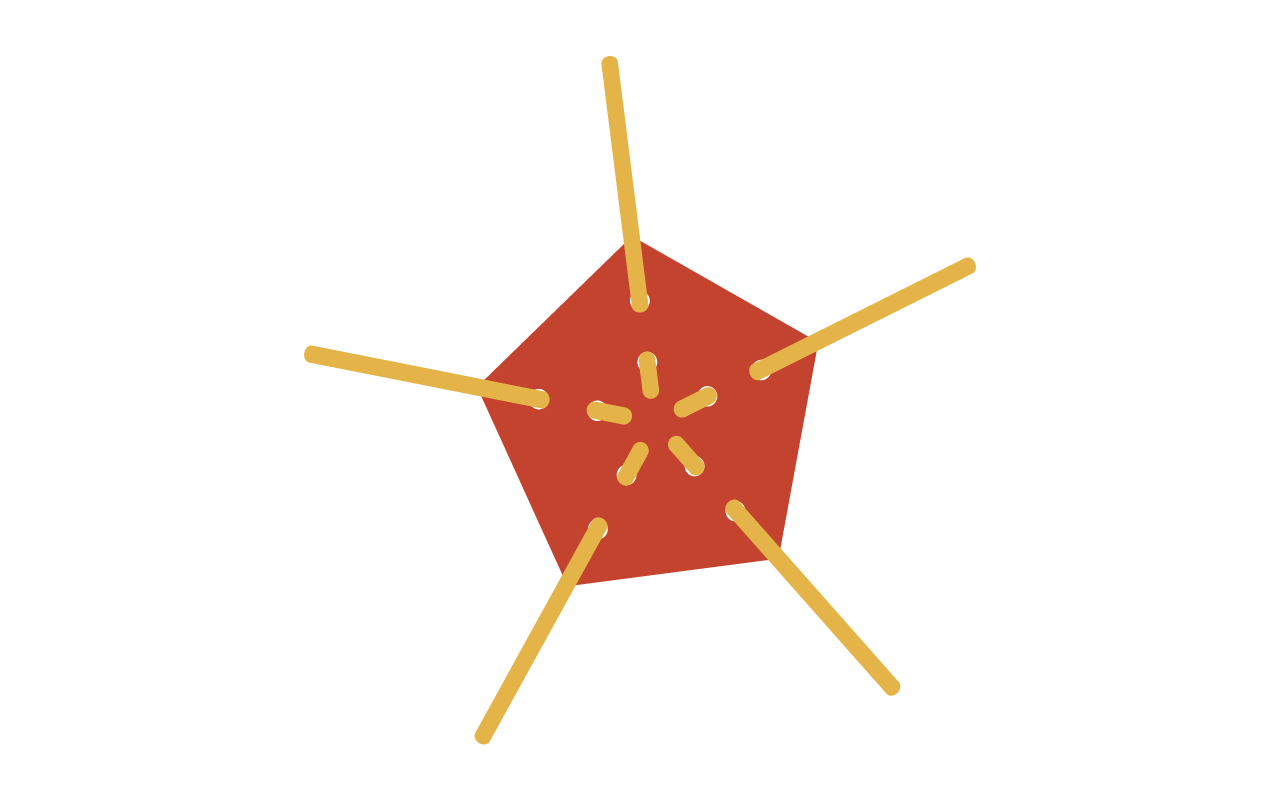
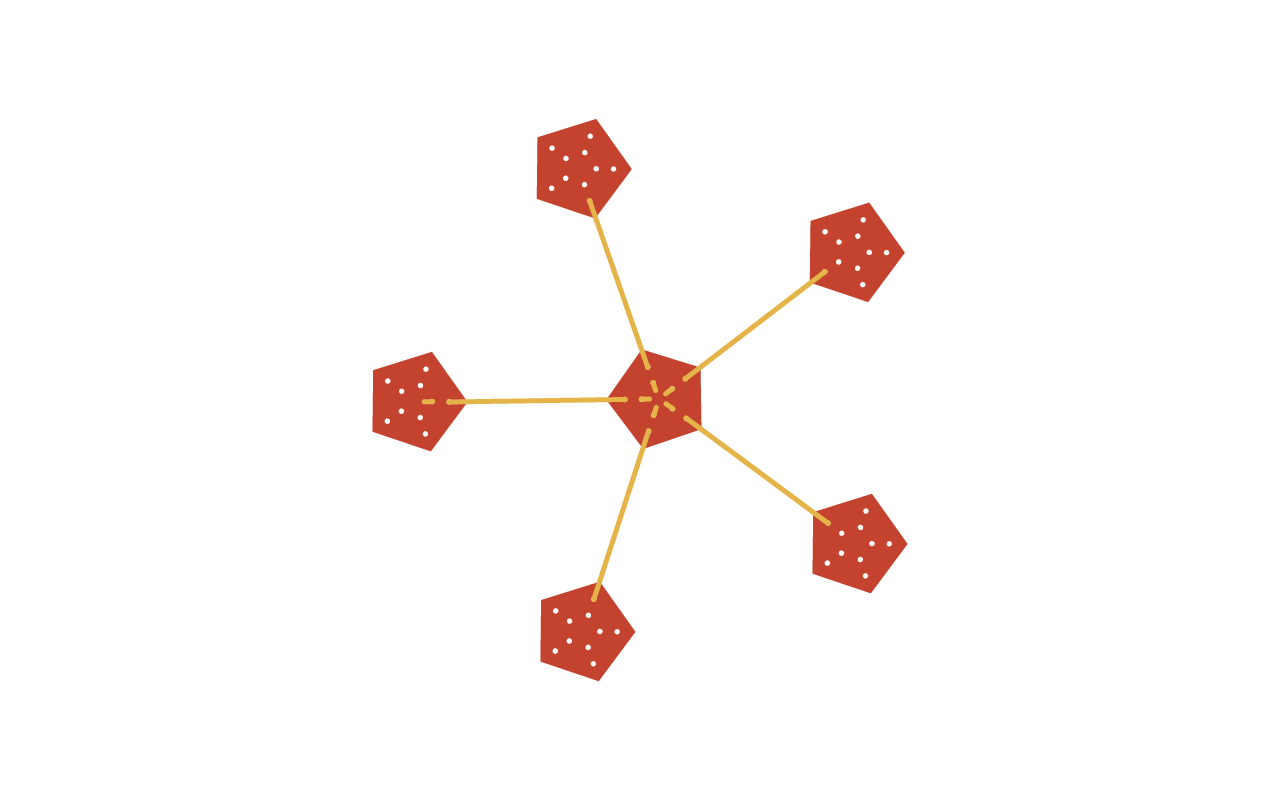
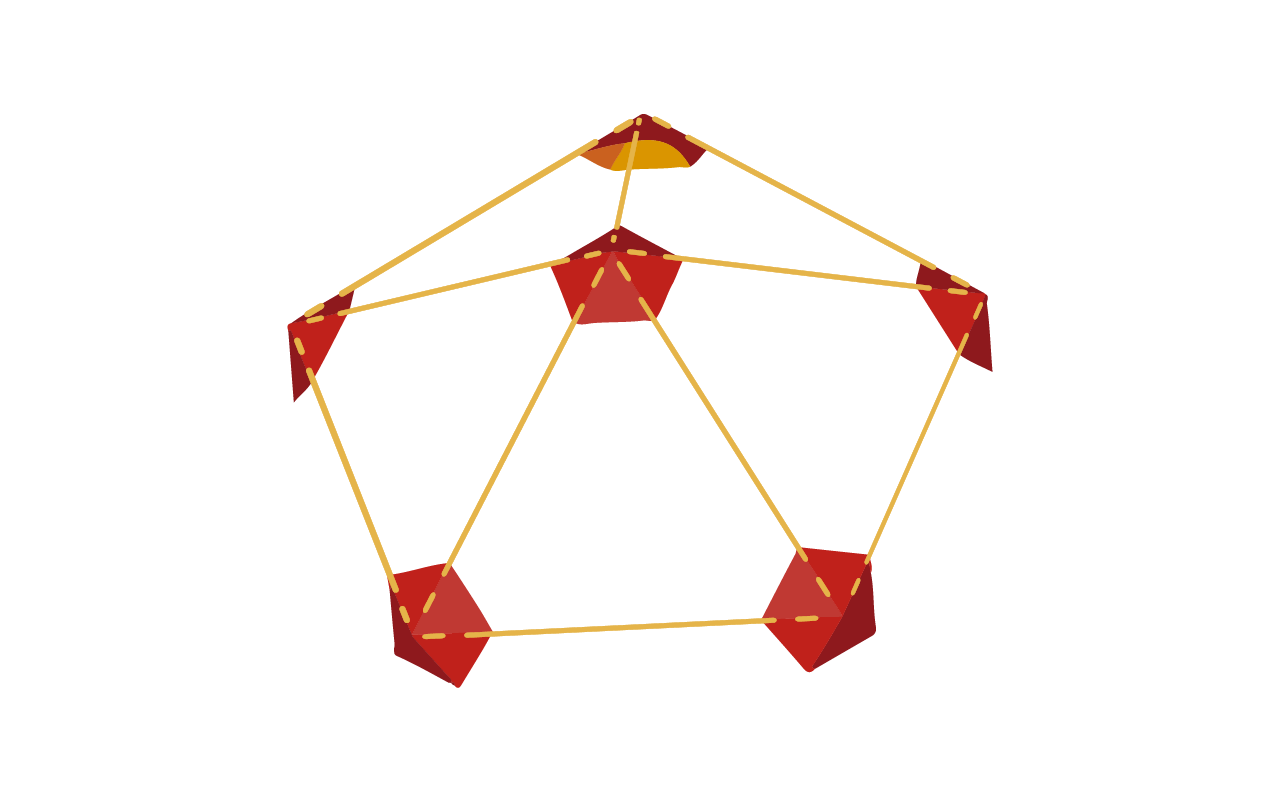
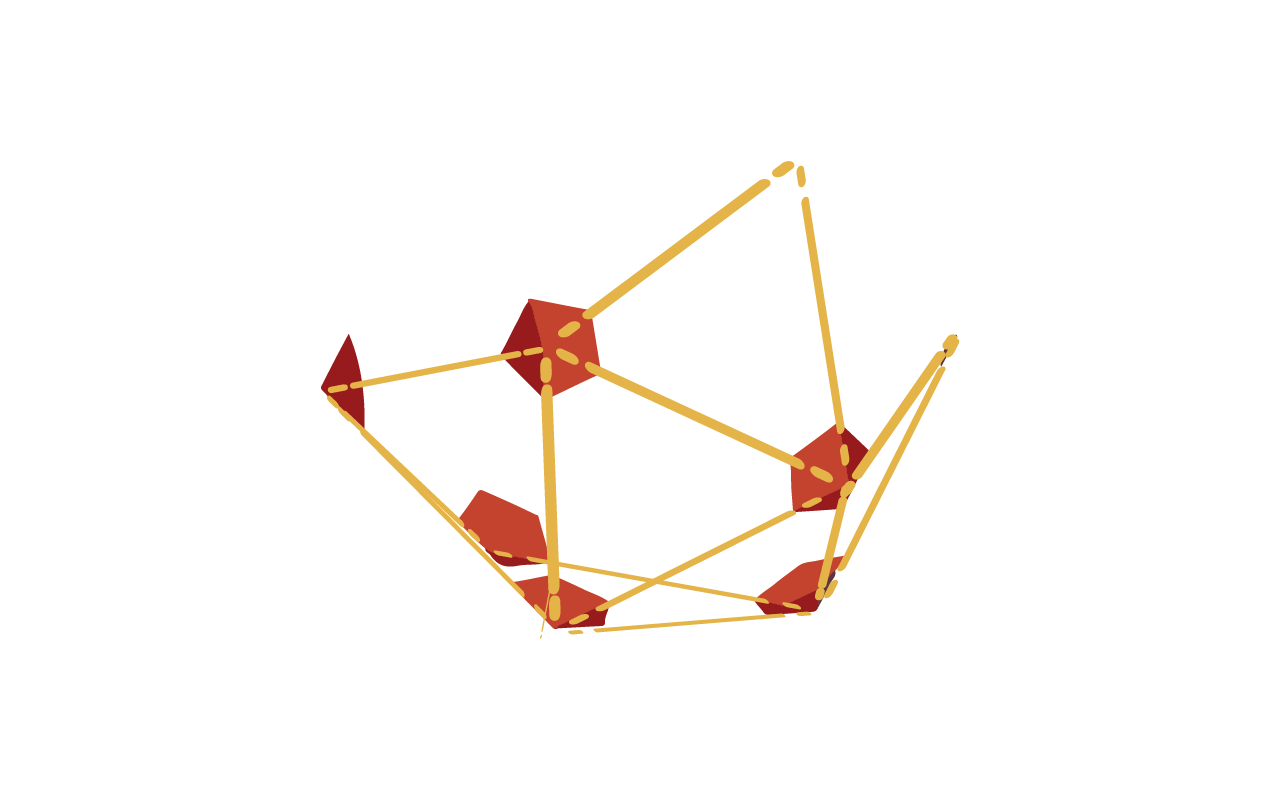
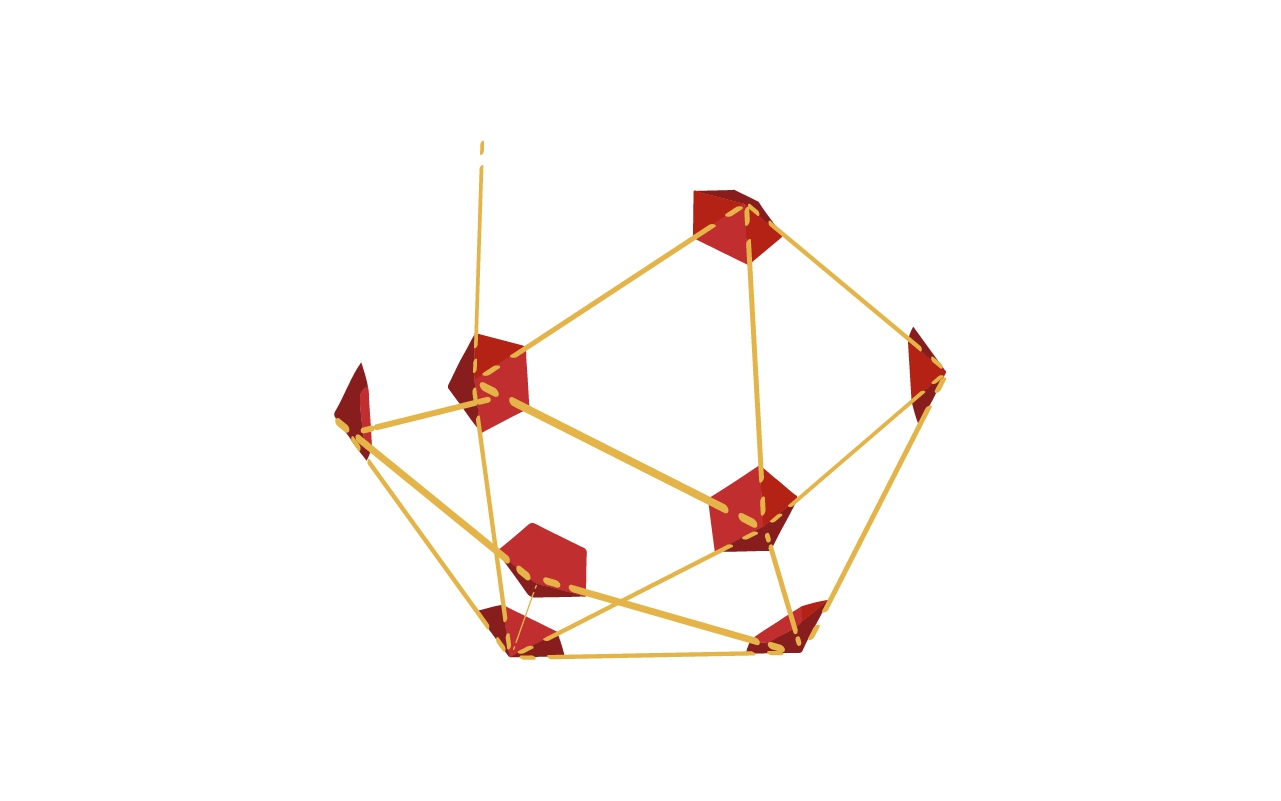
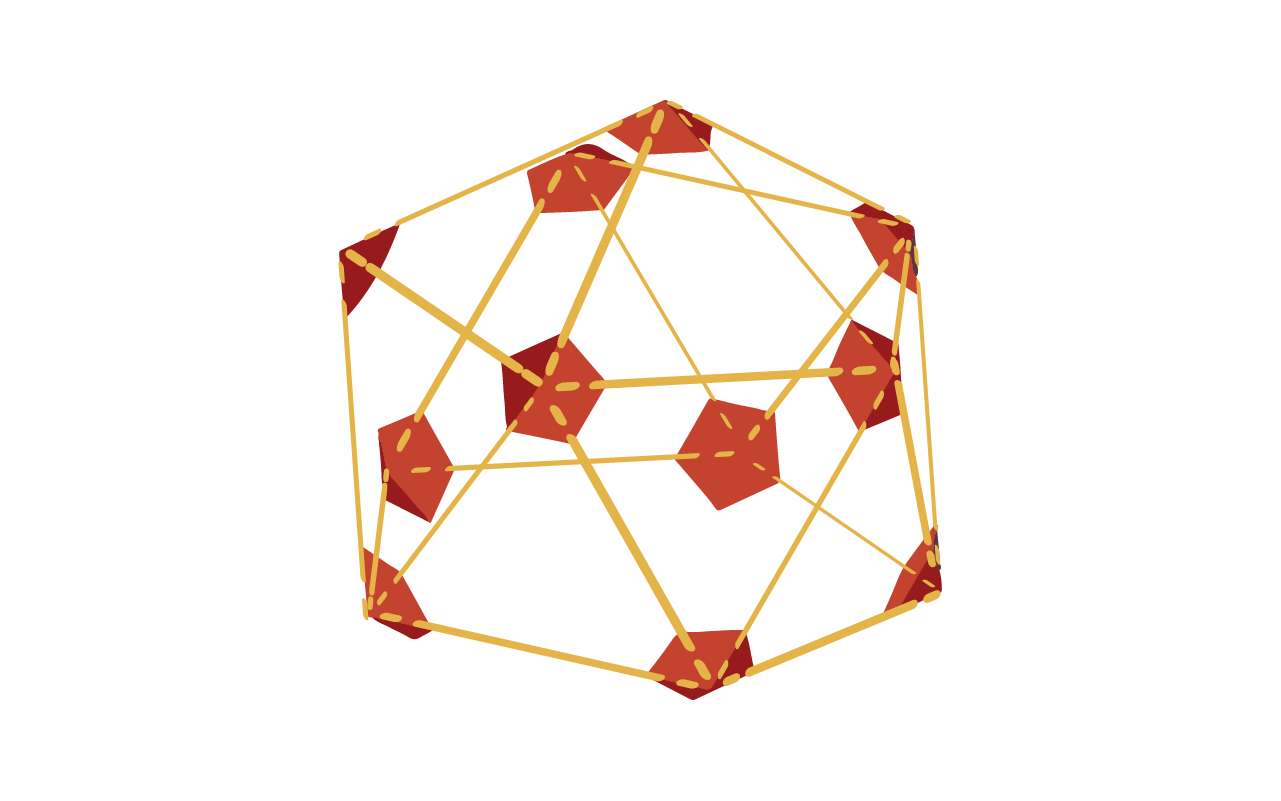
Montar o icosaedro
Esse projeto destina-se a você aprender a construir o icosaedro!
O sólido platônico mais complexo tem 30 arestas, 12 vértices e 20 faces. Por ter tantos componentes, parece uma "bola" ou esfera. Na verdade, é comumente usado como ponto de partida para cúpulas geodésicas, um tipo de estrutura arquitetônica inovadora com características arredondadas. Eles foram desenvolvidos pelo gênio Buckminster Fuller no início do século XX.
MATERIAIS NECESSÁRIOS:
- 12 conectores pentagonais
- 30 varetas
- 60 tiras elásticas
Baixar conteúdos
FICHA TÉCNICA
- Duração: 45'
- Disciplina:
- Matemática – Polígonos: classificações quanto ao número de vértices, às medidas de lados e ângulos e ao paralelismo e perpendicularismo dos lados.
Relações entre arcos e ângulos na circunferência de um círculo.
- Artes – Elementos da linguagem.
- Língua – Produção de texto oral.
- Nível de dificuldade: Médio.
- Licença: Creative Commons 4.0 atribução.
- Créditos: Tati Tabak, Fernando Daguanno, Carlos Vidal, Luciana Squeri, Léo Melo, Alquimétricos 2020/2021
Pré-requIsitos
- ANTES DE COMEÇAR
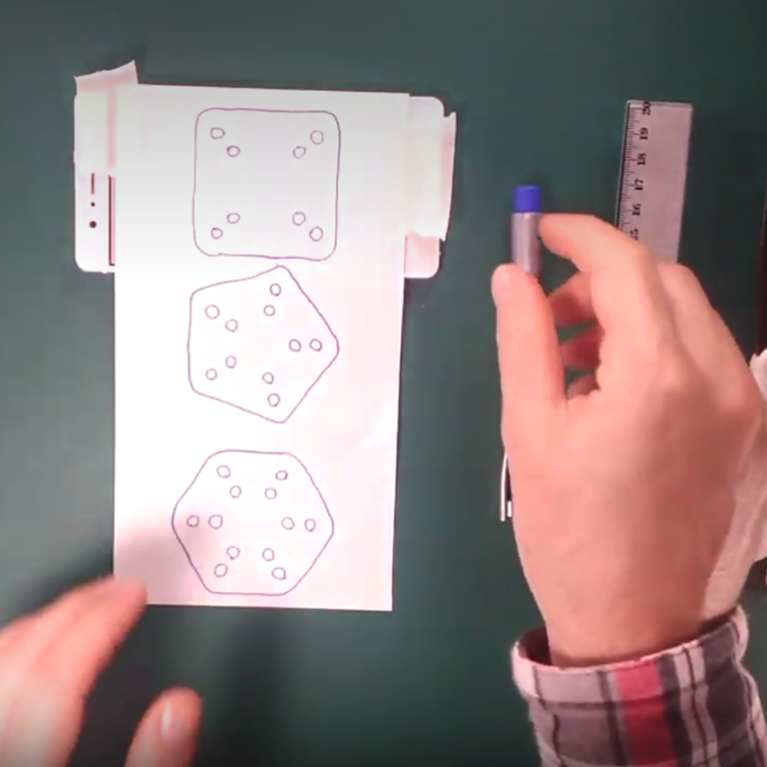
Todo o que você precisa saber para escolher e utilizar corretamente materiais e ferramentas. - TRAÇAR GABARITOS
No caso que não tenha como imprimir o design dos gabaritos fornecidos. - FABRICAR GABARITOS
Sempre é bom ter distintos gabaritos prontos antes de começar a produzir conectores} - FABRICAR CONECTORES
Pode produzir todos os conectores alquimétricos que quiser com esse simples tutorial.
BNCC
Assista o vídeo
Acompanhe as instruções detalhadas para fabricar conectores Alquimétricos usando tesoura e alicate vazador
Instruções passo a passo: Conectores
01
Pegue um conector pentagonal e enrosque uma haste passando-o pelos dois orifícios que estão em um de seus vértices. Entrando acima da figura e saindo abaixo.
02
Passe mais quatro hastes da mesma maneira, completando todos os vértices do pentágono.
03
Coloque os conectores nas extremidades livres de cada uma das cinco hastes usadas. Sempre enfie da mesma maneira
04
Junte dois conectores com cinco novas hastes, formando um pentágono. Use os vértices adjacentes para passar as hastes.
05
Coloque dez hastes nos dois vértices livres que cada um dos pentágonos deixou.
06
Junte duas hastes, as mais próximas, com um novo conector, um total de cinco são necessárias.
07
Junte dois conectores com cinco novas hastes, formando um novo pentágono. Use os vértices adjacentes para passar as hastes, àquelas usadas anteriormente.
Essa figura com base plana se chama de domo geodésico, e virou uma nova tendência de arquitetura sustentável nas últimas décadas.
08
Coloque as últimas 5 hastes nos únicos vértices livres restantes em cada conector. E junte todos eles colocando o último conector pentagonal.
ATENÇÃO:
Lembre-se que existe uma grande possibilidade de a haste cortada sair rapidamente ao ser cortada, com risco de ferir alguém ou causar algum problema. Você pode tentar prender os dois lados da vareta com os dedos ou com a ajuda para que ela não voe.
Você também pode prender na mesa com fita ou pedir a ajuda de outra pessoa para segurá-los enquanto você os corta.
Para continuar aprendendo
Esta ação pode ser usada para fazer certas trocas relacionadas a:
Aproximações da circunferência
- Reconhecer alguns elementos que permitem uma aproximação à noção de esfera, tais como: corda, raio, diâmetro.
- Relação com uma bola.
Elementos gráficos e formas geométricas
- Explorar, reconhecer e identificar os elementos visuais: ponto, linha, forma, espaço, relevo, movimento, volume bidimensional e tridimensional, tanto na figura construída como nos objetos da casa com os quais esta figura pode ser comparada.
Leitura e escrita
- É possível refletir sobre a importância de identificar os aspectos centrais de uma lista de etapas e testar as derivações da alteração na ordem das instruções.
- Diferentes estratégias podem ser trabalhadas para a elaboração de instruções para a montagem do tetraedro, pensando em diferentes situações e leitores.
