O Guarda-chuva
O objetivo deste projeto é que você aprenda a construir um objeto que simule o funcionamento de um guarda-chuva.
Com isso, você poderá aprender como, através da alquimetria, você pode projetar, imitar ou replicar mecanismos que estão presentes em vários objetos do cotidiano, graças à versatilidade que o Alquimétricos tem para combinar suas conexões.
MATERIAIS NECESSÁRIOS
BAIXAR CONTEÚDOS
FICHA TÉCNICA
PRÉ-REQUISITOS
BNCC
Passo a Passo
1
Faça um furo com o furador no centro de ambos os conectores hexagonais.
2
Passe uma vareta de costela (a de 22 cm) por dois dos orifícios de um conector linear, de forma côncava.
3
Passe uma vareta extensora (um de 15 cm) pelos outros dois orifícios do mesmo conector linear, mas desta vez de forma convexa.
O conector linear deve se parecer com um S.
4
Da mesma forma, repita as etapas 2 e 3 com todos os conectores lineares restantes.
5
Faça uma trava com um elástico próximo a uma das pontas do bastão (35 cm).
6
Coloque um dos hexágonos (o verde) na parte mais curta da haste do bastão através do furo central feito no passo 1, até fixar na trava.
7
Insira as estruturas lineares feitas no passo 6, as estruturas lineares feitas na ponta das varetas costela (22 cm) de forma côncava no hexágono verde do passo anterior.
8
Repita esta ação com as outras 6 estruturas lineares.
9
Coloque o segundo hexágono (o roxo) no bastão e deslize-o aproximadamente até a metade do orifício central feito na etapa 1.
10
Coloque as 6 estruturas lineares das varetas raios (15 cm) no hexágono roxo da etapa 9, de forma convexa.
11
Aproxime os conectores lineares e verifique se eles estão na mesma distância
12
Opcional. Faça uma cobertura, colocando uma estrutura circular com o centro recortado na parte superior do bastão, que pode ser feito de algum material flexível (tecido, papel) e, se necessário, dobre previamente de modo que marque 24 triângulos.
Trave com o hexágono superior (o verde).
Para continuar aprendendo
Em casa
Você pode fazer diferentes capas para o guarda-chuva, variando o tipo de material, a cor e observando as diferenças em relação à passagem de luz ou água.
Pode pendurar tiras de papel nas bordas de cada haste para decorá-lo e realizar jogos e danças inspirados na maneira como a decoraram.
Pode fazer desenhos na parte interna da capa do guarda-chuva, como uma decoração semelhante ao céu, ou segmentos de cores diferentes que, ao serem girados, se sobrepõem e aparecem em outra cor.
Na escola
É possível olhar para o guarda-chuva e encontrar diferentes figuras planas, como triângulos, círculos, ou as figuras que poderiam potencialmente ser observadas, como um hexágono, e trabalhar com as propriedades geométricas dessas figuras e as relações entre elas. Por exemplo, os triângulos simétricos que compõem o possível hexágono, as nervuras do guarda-chuva, que se atingem a borda exata do telhado, representam os raios da circunferência.
Você podem colocar uma folha escura em uma projeção do céu, copiar com giz algumas estrelas brilhantes ou especificamente as estrelas principais de uma constelação escolhida e fazer buracos nelas para depois usar como capa para ter um guarda-chuva estelar toda vez que for apontado para um luz. Também pode ser usado à noite, combinando-o com a constelação real observada.
Outra possibilidade é realizar um exercício matemático de proporcionalidade com o aumento ou redução do tamanho das hastes e posteriormente comparar o tamanho da circunferência de cobertura, para calcular se ela é ampliada ou reduzida com a mesma relação proporcional, mantendo sua taxa de variação.
Podem analisar a relação entre as propriedades do material e a função dentro do objeto, observando, por exemplo, a necessidade de peças rígidas ou flexíveis. Por sua vez, eles podem modificar o material de cobertura, por exemplo, para comparar materiais permeáveis, semipermeáveis e impermeáveis ou para ver quais são transparentes, translúcidos ou opacos.
Também podem fazer uma capa usando as cores do disco de newtons ou pares de cores complementares e girar o guarda-chuva observando a cor que se aparece ao girá-lo com certa velocidade.
Outra opção é decorar o guarda-chuva e usá-lo dentro de uma coreografia ou como elemento de uma peça teatral.
Você sabia?
A Ravenala madagascariensis ou árvore do viajante, é chamada desta maneira porque qualquer viajante sedento na ilha de Madagascar, pode encontrar água depositada em muitas partes da planta. Como nos folíolos e no interior das folhas, além das brácteas das flores.
Cada planta pode armazenar até um quarto de litro de água.
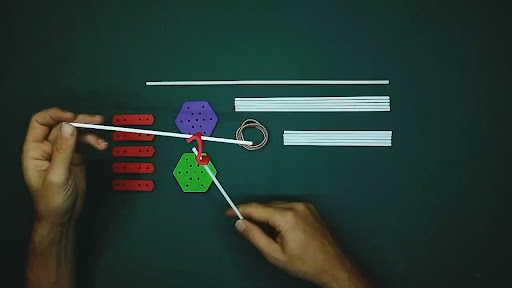
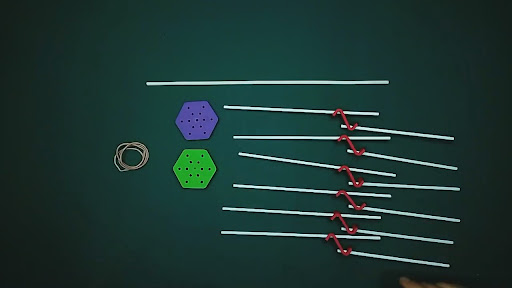
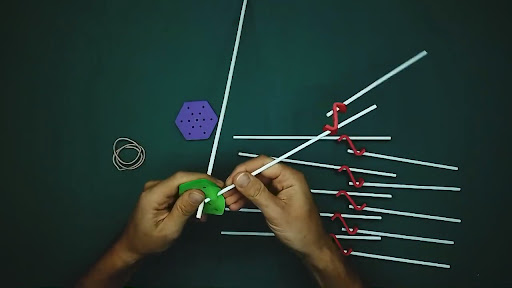
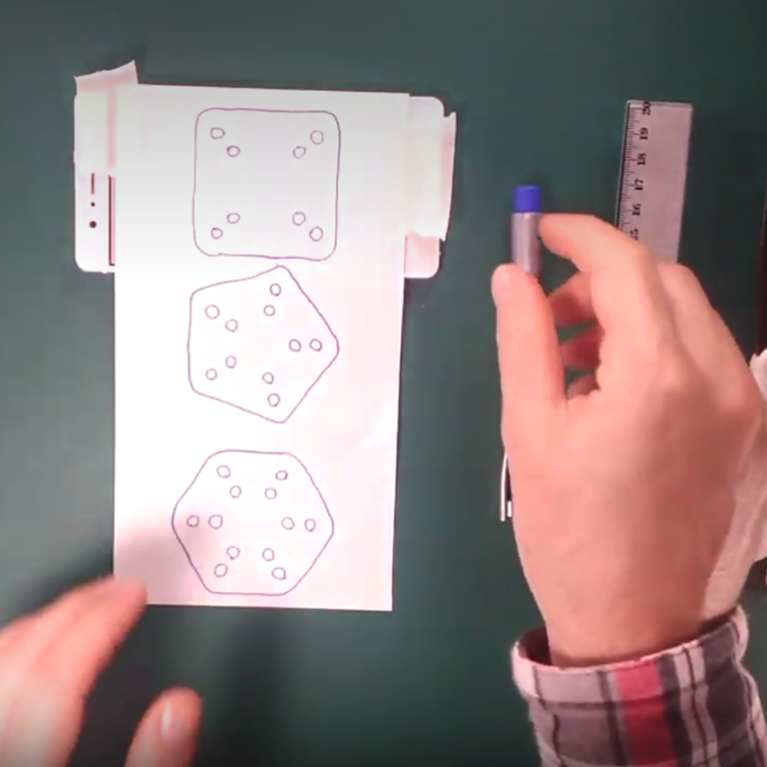
Cool!
A haste de 35 cm não encontrei, então peguei um pedaço de bambu e fiz. Ficou muito bom.
Inspirado no trabalho do Murilo uma tarde de chuva em SESC Itaquera, SP. 7 de outubro de 2017
https://photos.app.goo.gl/iLnYvttNe6wkCgTU8
Amei fazer o guarda chuva!!
Abriu meus olhos para novas possibilidades, tanto do básico, como um sólido geométrico, quanto em possibilidades mais complexas, como o mecanismo de uma garra envolvendo conceitos de robóticas. E a cada projeto realizado, há um amadurecimento em nossos pensamentos para desenvolver e elaborar novos projetos, assim como os estudantes conseguem ter esse amadurecimento quando aplicamos esses projetos em nossas aulas.
https://drive.google.com/file/d/1VSSxcibxXBWE759utbeHD4yjCCDDR17L/view?usp=sharing